Thermodynamics of Rubber-like Elasticity

In experiments concerning the relationships between length, temperature, and

force, usually the change in force with temperature at constant length is recorded.It is therefore necessary to extend the thermodynamic treatment of the elasticity. Moreover, the force is not purely entropic, and the energetic contribution carries useful information on the dependence on temperature of the average end-to-end distance of the network chains in the unstrained state. It is therefore important to know how to deduce these quantities from a thermoelastic experiment.

The change in internal energy during stretching an elastic body is

dU=dQ?dW

where dQ is the element of heat absorbed by the system and dW the element of work done by the system on the surroundings. In a reversible process,

dQ=TdS

where S is the entropy of the body. The work dW can be expressed as the sum

?dW= ?pdV + f dL

where p is the equilibrium external pressure, dV the volume dilation accompanying

the elongation of the elastomer, and f the equilibrium tension. Thus,

dU=TdS? pdV + f dL

At constant pressure, the enthalpy change is

dH=dU+ pdV =TdS+ f dL

A deformation dL at constant pressure and temperature induces a retractive force

(*)

Expression (*) is one of the forms of the thermodynamic elastic equation of state.

Measurements of stress at constant length as a function of temperature . An equation similar to equation (*) is obtained for the elastic force measured at constant volume:

The variation in the Helmholtz free energy has the following expression:

dA= ?SdT? pdV + f dL

if v=cte

(***)

Thus, equation (**) can be written as

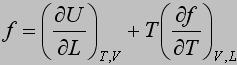
The energetic and entropic components of the elastic force, f _e and f _s, respectively, are obtained from thermoelastic experiments using the following equations:

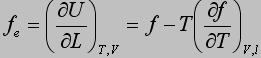
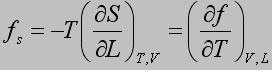
Statistical Treatment of Rubber-like Elasticity show:

by equation (***)

Benyamin jafaryan  

22-Nov_2008